|
In Part 1, I wrote about the different kinds of test scores. In Part 2, I'll explain how to interpret those scores. As I said in Part 1, I prefer to use standard scores to gauge progress because they’re on an equal interval scale. But what do they mean? To assist with this discussion, consult the diagram below from Part 1:
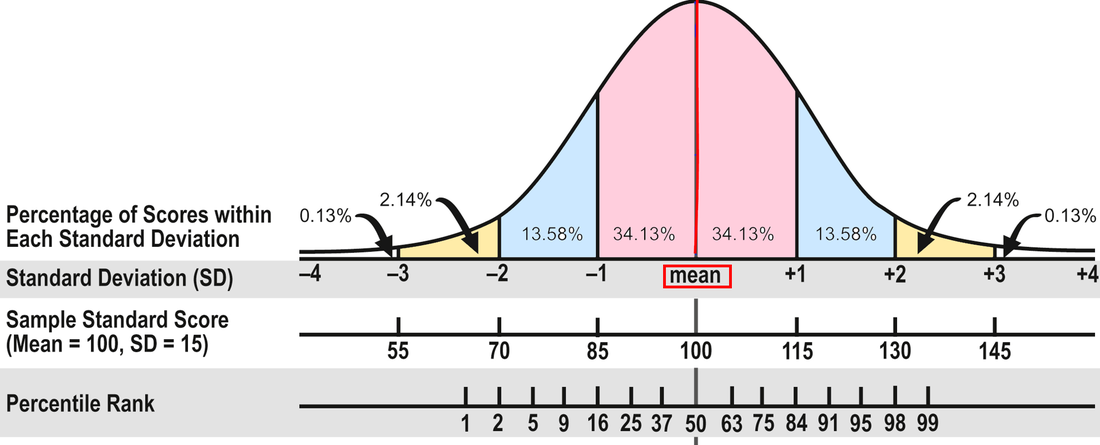
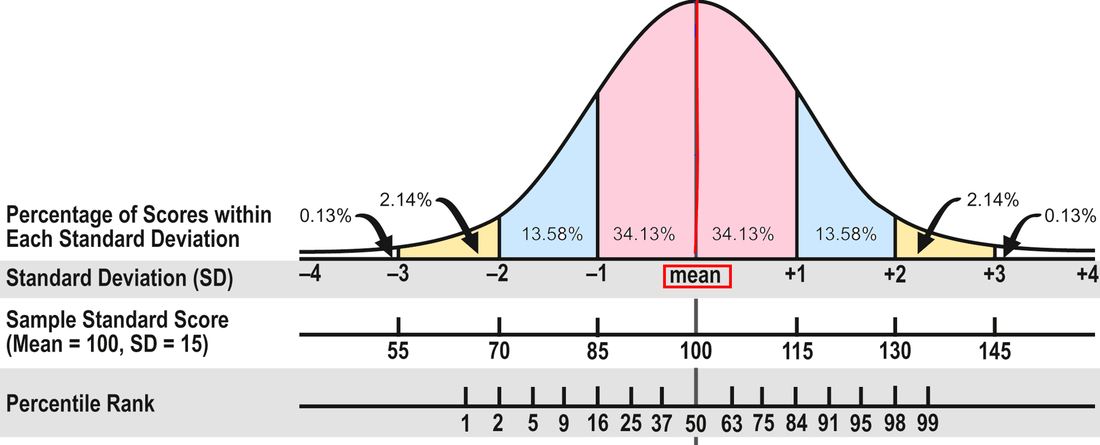
The Average Range. To review, about 68 percent of the people who take a standardized test will obtain scores within plus or minus one standard deviation (explained in Part 1). The Wechsler and Stanford-Binet intelligence tests designate the middle 50 percent of the area between plus or minus one standard deviation as the Average range--or 90 to 109 for tests with a mean of 100 and standard deviation of 15. That's the area that many evaluators consider Average, including me. In other words, half the students taking the test will have scores within the Average range and half will have scores that are above or below Average.
However, some researchers and clinicians consider the full 68 percent to be in the Average range, or scores between 85 and 115. Neither interpretation is right or wrong because there isn't agreement in the field. In my opinion, it makes more sense to use the 50 percent figure; it doesn't seem to me that the scores of almost two-thirds of the population are in the Average range. If 90 to 109 is Average, 80 to 89 is Below Average and 110 to 119 is Above Average. (FYI, psychologists use the terms Low Average and High Average for Below and Above Average.) It might help you keep track if you make a simple chart of these scores. For example:
Confidence Bands. Moving on from the scores themselves, have you heard people talk about confidence bands? That's an important concept to understand because a single testing may not demonstrate a student's true score, his or her actual ability. The true score is a statistical concept and too complicated to explain here, but the point to understand is that there is some error, some uncertainty, in all testing--in the test itself, in the testing conditions, in the student's performance, and so on. To account for this uncertainty, a confidence band is constructed to indicate the region in which a student's true score probably falls. Evaluators can select different levels of confidence for the bands; I use 90 percent. Therefore, I provide a confidence band that indicates the region in which a student's true score probably falls 90 times out of 100. Test publishers usually compute these for users.
Here's an example. Mary obtained a standard score of 97 on a reading test, which is solidly in the Average range (90 to 109). However, although the obtained score on a test gives the best single estimate of a student's ability, a single testing may not necessarily demonstrate the true score. Mary's standard score confidence band is 91 to 104. Subtests and Scaled Scores. Many tests measure different parts of a domain with component tests called subtests. Sometimes the subtests yield scaled scores, which are standard scores that range from 1 to 19 points with a mean of 10 and a standard deviation of 3. Scaled scores between 8 and 12 are considered Average. Composite Scores. Subtest scores may stand alone if they have high statistical reliability. If not, they should only be reported as part of a composite score. A composite score is computed by combining related subtests--for example, subtests that assess word recognition and reading comprehension or math computation and applications. Because composite scores are generally more statistically reliable than subtest scores, they are sometimes the only score that should be considered. However, it is better to use tests with highly reliable subtests when they are available because composite scores can mask the differences among the subtest scores. For example, Richard obtained these subtest scores on a recent reading test: Word Recognition, 73; Pseudoword Decoding, 78; and Reading Comprehension, 107. The 73 and 78 scores were in the Borderline range (70-79), and the 107 was in the Average range. The composite score was 82, in the Below Average range. However, none of the three subtests was Below Average. Because of the variability between the word recognition and decoding scores on the one hand and the comprehension score on the other, it would have been more accurate to not provide a composite score in this case. Here's another example. Nalia obtained two math scores recently: 100 in Math Applications (Average range) and 84 in Math Computation (Below Average) with a composite score of 90, which is at the bottom of the Average range. However, there was a 16-point difference between the two subtest scores, and it would be incorrect to say that Nalia's math performance was in the Average range when she was struggling with computation. Yet sometimes this kind of difference isn't explained in an evaluation report, so you'll need to read carefully and critically. I've presented quite a bit of technical information in this blog post. Please let me know in the Comments below if you have any questions! And feel free to share any ideas you have for future posts.
0 Comments
In Part 1, I discuss the different kinds of test scores and what they mean and don't mean. In Part 2, I'll address how to interpret scores--what's considered average, confidence bands, the differences between composite and subtest scores, and so on. The array of test scores in an evaluation report can be confusing. On standardized tests, the number correct is called the raw score. A raw score by itself is meaningless because it’s not the percentage correct; it’s just the number correct, and different tests have a different number of items. So publishers convert the raw scores into derived scores to compare a student’s performance to that of other students his age in the norm group—the people the test was standardized on. There are several kinds of derived scores. Before I discuss a few of them, I need to introduce some statistics. I know this is technical, but bear with me because it will help in the end! Most psychological and educational test results fall within the normal or bell shaped curve. The normal curve is divided into standard deviations that measure the distance from the mean (the average score). In the diagram below, you can see that about 68 percent of the population will have scores between plus and minus one standard deviation (pink area). An additional 27 percent will have scores between plus/minus two standard deviations (about 95 percent; pink and blue areas). And 4 percent more will have scores between plus/minus three standard deviations (about 99 percent; pink, blue, and yellow areas). Now pat yourself on the back for getting through this section!
|
AuthorDr. Andrea Winokur Kotula is an educational consultant for families, advocates, attorneys, schools, and hospitals. She has conducted hundreds of comprehensive educational evaluations for children, adolescents, and adults. |