UNDERSTANDING TEST SCORES, PART 1

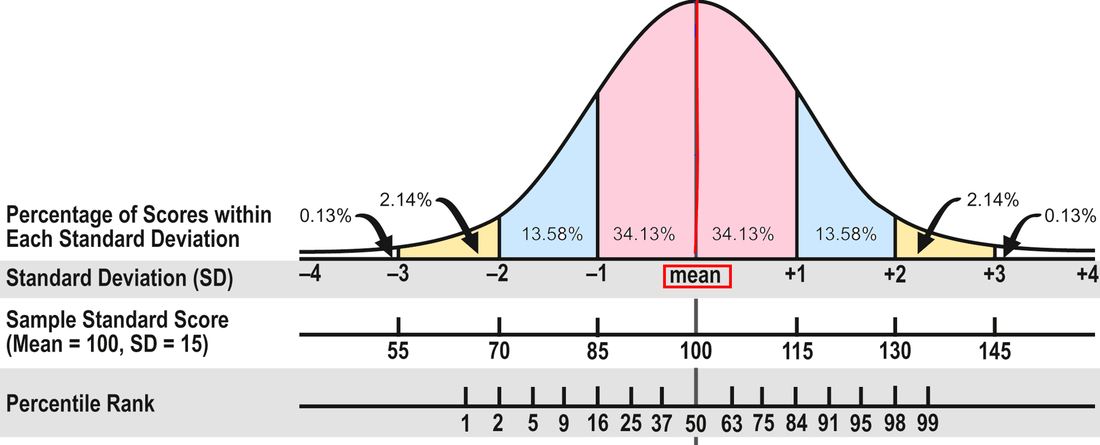
In Part 1, I discuss the different kinds of test scores and what they mean and don't mean. In Part 2, I'll address how to interpret scores--what's considered average, confidence bands, the differences between composite and subtest scores, and so on.

The array of test scores in an evaluation report can be confusing. On standardized tests, the number correct is called the raw score. A raw score by itself is meaningless because it’s not the percentage correct; it’s just the number correct, and different tests have a different number of items. So publishers convert the raw scores into derived scores to compare a student’s performance to that of other students his age in the norm group—the people the test was standardized on. There are several kinds of derived scores. Before I discuss a few of them, I need to introduce some statistics. I know this is technical, but bear with me because it will help in the end!
 
Most psychological and educational test results fall within the normal or bell shaped curve. The normal curve is divided into standard deviations that measure the distance from the mean (the average score). In the diagram below, you can see that about 68 percent of the population will have scores between plus and minus one standard deviation (pink area). An additional 27 percent will have scores between plus/minus two standard deviations (about 95 percent; pink and blue areas). And 4 percent more will have scores between plus/minus three standard deviations (about 99 percent; pink, blue, and yellow areas). Now pat yourself on the back for getting through this section!

The reason we care about all this is because some derived scores are better than others, depending on your purpose. When interpreting test results, I prefer standard scores because they fall along an equal interval scale. Many educational and psychological tests--including the Wechsler intelligence tests--have a mean of 100 and a standard deviation of 15, so I'm using that mean and standard deviation on the diagram above and for this blog post. That means that there will always be 15 points between any two standard deviations. And because of the equal interval scale, we can compare scores across tests given in different years and across different tests that have the same mean and standard deviation. For example, we can compare an educational test to an IQ test or to a different educational test.

Now let’s look at percentile rankings. A percentile ranking means that the score exceeds a particular percent of the other scores obtained by students of the same age in the normative sample. For example, I can say that a student obtained a standard score of 100, which is better than 50 percent of the students his age in the normative group. In other words, I can use a percentile ranking to explain a standard score. But be aware that percentile rankings are not on an equal interval scale, and they’re widely misused and misunderstood. I'll explain.

First, a percentile ranking is NOT the percentage correct. It has nothing to do with the correct vs. incorrect responses to the test. Second, because percentiles don’t have equal distances between units, they can’t correctly be added or subtracted to indicate growth or lack of growth. This is important. Let's assume that Julie obtained a standard score of 100 last year on her reading test. When she was retested recently, she obtained a score of 115. That's a difference of one standard deviation. The corresponding percentiles between Julie's two standard scores are 50 and 84 (see diagram above), or a change of 34 percentile rankings. Now look at the percentile differences between Alan's standard score of 70 last year and his recent retesting of 85, which is again a 15-point standard score gain--one standard deviation. However, Alan's corresponding percentiles are 2 and 16, or growth of only 14 percentile rankings. Note that the number of percentiles between Julie's two scores is different than between Alan's even though in both cases the scores are one standard deviation apart. When we examine the percentile rankings, it looks as if Alan didn't make much progress, doesn't it? There's only a 14-percentile gain compared to 34. But actually there isn't less growth. It's still a one standard deviation change. See what I mean? That's a problem with misinterpreting percentile rankings.

In addition, there’s more distance between percentile rankings as you get farther from the mean, in either direction. Look at Mark's standard score when he was tested the first time (55) and again two years later (70)--still 15 standard score points and one standard deviation between the two scores. Yet the percentile rankings range from only .1 to 2--just 1.9 percentiles! Think about that: The comparison between two scores will have a different meaning depending on the position on the percentile scale, another problem with comparing percentile rankings! Be careful when someone tells you there's a lot of growth (or conversely very little growth) between two percentile rankings. Instead ask to compare standard scores.

Now let’s look at my least favorite scores, grade or age equivalents. These are even more misused than percentiles. (For simplicity, I'll refer to grade equivalents, but the same arguments apply to age equivalents.) A grade equivalent indicates that the number of items that someone answered correctly is the same as the average score for students of that grade in the test standardization group; note that a grade equivalent does not indicate which items were correct or the level of the items.

Here are some of  the issues with using grade equivalents. (1) The use of grade equivalents leads us to make incorrect comparisons. Grade equivalents are usually divided into tenths of a grade, but a fourth grader with a 7.6 grade equivalent, for example, is probably not performing like seventh graders in their sixth month. Grade equivalents are not grade levels. The grade equivalent only means that the fourth grader shares the same number correct on the test—which is not the same thing as performing at the same grade level. (Sometimes those skills aren’t even taught in the grade equivalent grade.) (2) Publishers often determine many grade equivalents by interpolation or extrapolation, or both; there may not have been children at all the grade equivalents in the normative sample—and certainly not enough to be statistically sound. (3) Grade equivalents assume that growth is constant throughout the school year, which is probably not true. (4) Similar to the last point but slightly different: Academic growth flattens as children get older (less change), so the difference between grade equivalents at second and third grade, for example, is probably not the same as the difference between seventh and eighth grade scores.  (5) The same grade equivalent on different tests may not mean the same thing. In fact, grade equivalents vary from test to test, subtest to subtest within a test, and subject to subject.

Therefore, my advice is to use standard scores for most test interpretation and comparisons and use percentiles to explain standard scores. I truly believe we should ignore grade equivalents, and many national organizations suggest that we do just that, including the American Psychological Association and the International Literacy Association. Even test publishers often say that they include them only because some states require them.

Please comment below if this was helpful or if you have any questions. I'll continue this discussion in Part 2.